1.背景
在美团,为了保证单子质量,需要对上单系统创建的每一个产品进行审核。为了提高效率,审核人员积累提炼出了一套关键词库,先基于该词库进行自动审核过滤,对于不包括这些关键词的产品信息不再需要进行人工审核。因此,如何在页面中快速的检测是否包含了这些关键词就变得非常重要。
对于上述问题我们描述为如下的形式:
- 给定关键词集合P={p1,p2,……,pk},在目标串T[1…m]中找到出现了哪些关键词。
很容易想到的方法就是针对每个单词去匹配一遍,最后总结出都哪些单词匹配成功。
考虑KMP算法,单个关键词匹配的时间复杂度是O(|pk|+m),所以,所有关键词都匹配一遍的时间复杂度为O(|p1|+m+|p2|+m+…+|pk|+m)。令n=|p1|+…+|pk|,上式化简为O(n+km),因此,当关键词的数量变得非常多时,这种算法就变得无法忍受了。
Alfred V.Aho和Margaret J.Corasick在1974年提出了一个经典的多模式匹配算法-AC算法,这个算法可以保证对于给定的长度为n的文本,和模式集合P{p1,p2,…pm},在O(n)的时间复杂度内找到文本中的所有目标模式,而与模式集合的规模m无关。
2.AC算法详解
AC算法的具体实现方法就是创建一棵前缀树,根据被查找的目标字符串,从树的根节点开始往叶子节点逐字符匹配。在这个过程中,如果发生失配,要根据失配跳转点进行跳转,如果找到匹配的模式串则进行打印输出。AC算法在扫描文本时完全不需要回溯,如果只考虑匹配的过程,该算法的时间复杂度为O(n),也就是只跟待匹配文本的长度相关。
AC算法的实现可以由如下三个步骤构成:
- 构造前缀树
- 设置每个节点的失配跳转并收集每个节点的所有匹配模式串
- 对目标字符串进行搜索匹配
其间共用到三个函数:goto,fail,output。
步骤一:构造前缀树
这里我们考虑模式集合P={“he”,”she”,”his”,”hers”}。
首先是goto函数的建立,该函数决定了对于当前状态S和条件C,如何得到下一状态S’。为了构建goto函数,我们需要建立一个状态转移图,开始,这个图只包含一个状态0,然后通过添加一条从起始状态出发的路径的方式,依次向图中输入每个关键字keyword,新的顶点和边被加入到图表中,这样就产生了一条能拼写出关键字keyword的路径。
添加第一个关键词“he”得到下图,其中从状态0到状态2的路径就拼写出了关键字“he”;

接着添加第二个关键字“she”得到下图,输出“she”和状态5相关联;
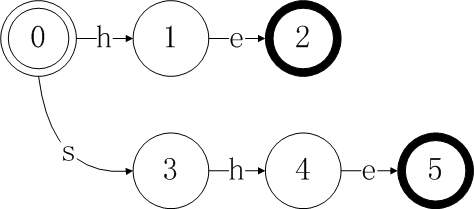
增加第三个关键字“his”得到下图,当我们增加“his”时,因为已经存在一条从状态0在输入h的条件下到达状态1的边,因此我们这里不需要另外添加一条同样的边。这个输出的“his”是和状态7相关联的;
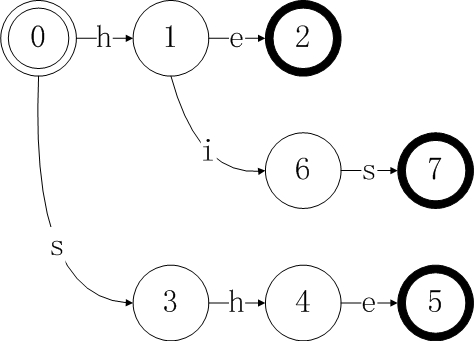
最后我们添加“hers”得到下图,输出“hers”和状态9相关联,最后对除了h和s外的每个字符都增加一个从状态0到0的循环;
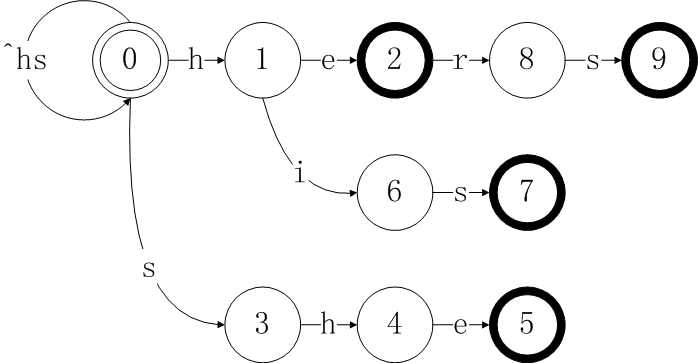
经由上面一系列添加过程,就构造了整个模式集合的状态转移图,这个图也就代表了转向函数goto。 我们利用伪代码将goto函数表示如下,同时我们在这一步骤中构造了output函数,但这个函数并不是完整的,需要在步骤二中继续完善:
begin
newstate ← 0
for i ← 1 util k do enter(yi)
for all a such that goto(0,a) == fail do goto(0,a) ← 0
end
procedure enter(a1a2…am):
begin
state ← 0
j ← 1
while goto(state, aj) ≠ fail do
begin
state ← goto(state, aj)
j ← j+1
end
for p ← j util m do
begin
newstate ← newstate + 1
goto(state, ap) ← newstate
state ← newstate
end
output(state) ← {a1a2…am}
end
步骤二:设置每个节点的失配跳转
失效函数fail决定了当goto函数得到的下一个状态无效时,应该回退到哪一个状态。在构造fail函数时,我们首先定义状态转移图中状态S的深度为从状态0到状态S的最短路径。以我们上面构造的状态转移图为例,起始状态的深度为0,状态1和3的深度是1,状态2、6、4的深度是2,依次类推。计算失效函数的思路是这样的:首先计算深度为1 的状态的失效函数值,然后是深度为2的,以此类推,直到所有状态的失效函数值都被计算出。同时,我们规定所有深度为1的状态的fail值为0,假设所有深度小于d的状态的fail值都已经计算出,考虑每个深度为d-1的状态r,基于这些已经被计算出的深度为d-1的fail值,我们是可以得到深度为d的fail值的。
令L(Si)为从根节点到Si节点的路径上的所有边的值的序列,我们从树的根节点开始遍历计算fail值,如果L(Sj)是L(Si)的一个后缀,并且是最长后缀,那么,fail(Si) = Sj。假设当前状态为S1,现在要求fail(S1),S1的前一状态我们记为S2,而S2跳到S1的条件为C,也就是S1 = goto(S2,C),而S2的fail值是已知的,记为S3,也即S3 = fail(S2),则L(S3)是L(S2)的一个最长后缀,假设S4 = goto(S3,C)存在,那么fail(S1) = S4,如果不存在则测试S5 = goto(fail(S3),C),直到得到一个有效的状态为止。这个计算的过程是这样的:
- 对于所有的字符a,如果goto(r,a) = fail,那么什么也不做(当r为我们上面构造的trie树的叶子节点时,就符合这种情况)
- 如果goto(r,a) == s,我们记state = fail®,执行state = f(state)零次或者若干次,直到使得goto(state,a) != fail,因为goto(0,a) != fail,所以这个状态是一定存在的。
- 记fail(s) = goto(state,a)。
我们还是以上面构造出的状态转移图为例,计算每个节点的fail值,根据规定,fail(1) = fail(3) = 0,因为1和3是深度为1的状态。
考虑深度为2的状态2、6、4: * 计算fail(2),令state = fail(1) = 0,由于goto(0,e) = 0,所以fail(2) = 0 * 计算fail(4),令state = fail(3) = 0,由于goto(0,h) = 1,所以fail(4) = 1 * 计算fail(6),令state = fail(1) = 0,由于goto(0,i) = 0,所以fail(6) = 0
考虑深度为3的节点8、7、5: * 计算fail(8),令state = fail(2) = 0,因为goto(0,r) = 0,所以fail(8) = 0 * 计算fail(7),令state = fail(6) = 0,因为goto(0,s) = 3,所以fail(7) = 3 * 计算fail(5),令state = fail(4) = 1,因为goto(1,e) = 2,所以fail(5) = 2
最后考虑深度为4的节点9: * 计算fail(9),令state = fail(8) = 0,因为goto(0,s) = 3,所以fail(9) = 3
这样一来我们构造的fail表如下:
| 状态 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| fail值 | None | 0 | 0 | 0 | 1 | 2 | 0 | 3 | 0 | 3 |
失效函数创建的伪代码如下:
begin
queue ← empty
for each a such that goto(0,a) = s ≠ fail do
begin
queue ← queue U {s}
fail(s) ← 0
end
while queue ≠ empty do
begin
let r be the next state in queue
queue ← queue - {r}
for each a such that goto(r,a) = s ≠ fail do
begin
queue ← queue U {s}
state ← fail(r)
while goto(state,a) = fail do state ← fail(state)
fail(s) ← goto(state,a)
output(s) ← output(s) U output(fail(s))
end
end
end
步骤三:对目标字符串进行搜索匹配
上面两个步骤都完成了之后就可以开始对目标串进行搜索了,只需对目标串从头到尾线性扫描,且没有回溯。搜索之前先记录树的当前节点node,初始时,树的当前节点node为根节点Root。从目标串的第一个字符开始,和Root的孩子节点进行匹配,如果不匹配,则目标字符串往后挪一个字符,继续在Root的孩子节点中查找匹配。如果找到匹配的孩子,则目标字符串往后挪一个字符,node变为匹配上的孩子节点。在接下来的匹配过程中,如果失配将跳转到node节点的fail值处继续进行匹配。在树上每次往孩子节点方向走一步都要检查该孩子节点的匹配模式串信息,如果有匹配的模式串信息,则应记录找到了哪些能够匹配的模式串。
整体的匹配过程如下代码所示:
begin
state ← 0
for i ← 1 until n do
begin
while goto(state,ai) = fail do state = fail(state)
state ← goto(state,ai)
if output(state) ≠ empty then
begin
print output(state)
end
end
end
3.上单系统中的实现
在美团上单系统中,待匹配的关键词根据产品类别进行分组,不同品类之间的关键词具有重叠。如果针对每个品类生成一棵状态转移树固然可行,但是随着品类的增多,对内存的使用也会随之增高。考虑到AC算法的时间复杂度与关键词的数量无关,因此可以考虑将所有品类的关键词构造在同一棵状态转移树中,每次进行匹配时,在output函数中对该关键词是否属于该品类做判断。在上单系统中,关键词用Keyword类表示,该类的定义如下:
public class Keyword implements Serializable {
private Integer id;
private Map<Integer, Integer> categoryTypeMap;
private String word;
private List<Integer> categories; //当前的关键词属于哪几个分类
getter and setter ...
@Override
public boolean equals(Object o) {
if (this == o) return true;
if (o == null || getClass() != o.getClass()) return false;
Keyword keyword = (Keyword) o;
if (id != null ? !id.equals(keyword.id) : keyword.id != null) return false;
return true;
}
@Override
public int hashCode() {
return id != null ? id.hashCode() : 0;
}
}
其中,categoryTypeMap属性用来标识该关键词在不同品类中所代表的类型,当匹配命中时,根据类型信息指出其可能违反了哪些条款。
我们用一个Node类来代表状态转移树的一个节点,同时,将goto信息、fail信息和output信息封装到里面,这样,这个类的定义就像下面这样:
static class Node{
int state; //自动机的状态,也就是节点数字
char character = 0; //指向当前节点的字符,也即条件
Node failureNode; //匹配失败时,下一个节点
List<Keyword> keywords; //匹配成功时,当前节点对应的关键词
List<Node> children; //当前节点的子节点
...
}
我们用Patterns类来表示整个待匹配的模式串,它是对Node的进一步封装:
public static class Patterns{
protected final Node root = new Node();
protected List<Node> tree;
public Patterns(List<Keyword> keywords) {
tree = new ArrayList<Node>();
tree.add(root);
for(Keyword keyword : keywords){
addKeyword(keyword);
}
setFailNode();
}
public void addKeyword(Keyword keyword) {
char[] wordCharArr = keyword.getWord().toCharArray();
Node current = root;
for(char currentChar : wordCharArr){
if(current.containsChild(currentChar)){
current = current.getChild(currentChar);
} else {
Node node = new Node(table.size(), currentChar, root);
current.addChild(node);
current = node;
tree.add(node);
}
}
current.addKeyword(keyword);
}
public void setFailNode(){
Queue<Node> queue = new LinkedList<Node>();
Node node = root;
for (Node d1 : node.children)
queue.offer(d1);
while (!queue.isEmpty()) {
node = queue.poll();
if (node.children != null) {
for (Node curNode : node.children) {
queue.offer(curNode);
Node failNode = node.failureNode;
while (!failNode.containsChild(curNode.character)) {
failNode = failNode.failureNode;
if (failNode.state == 0) break;
}
if (failNode.containsChild(curNode.character)) {
curNode.failureNode = failNode.getChild(curNode.character);
curNode.addKeywords(curNode.failureNode.keywords);
}
}
}
}
}
}
在上单系统中对关键词的匹配需要传递一个categoryId,当匹配成功时,我们需要根据传递的类别信息判断是否应该保存当前关键词:
public Set<Keyword> searchKeyword(String data, Integer category) {
Set<Keyword> matchResult = new HashSet<Keyword>();
Node node = patterns.getRoot();
char[] chs = data.toCharArray();
for(int i=0; i < chs.length; i++){
while (!node.containsChild(chs[i])) {
node = node.failureNode;
if (node.state == 0) break;
}
if(node.containsChild(chs[i])){
node = node.getChild(chs[i]);
if(node.keywords != null){
for(Keyword pattern : node.keywords){
if (category == null) {
matchResult.add(pattern);
} else {
if (pattern.getCategories().contains(category)) {
matchResult.add(pattern);
}
}
}
}
}
}
return matchResult;
}
算法的测试结果如下:
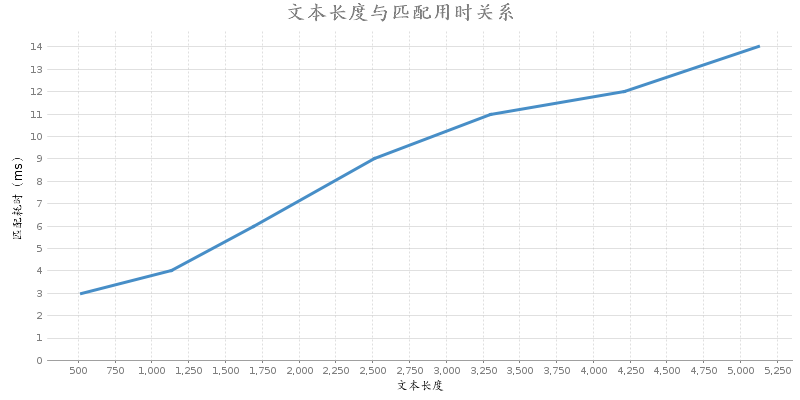
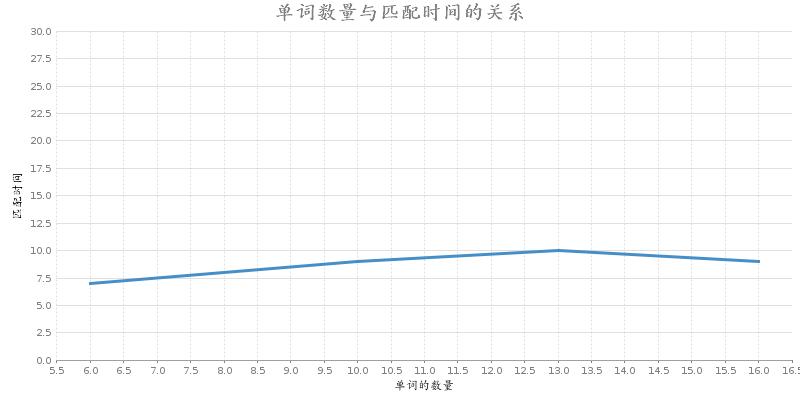
在第二张图中,有一个因素没有考虑进去,就是同样关键词数量,当关键词在文本中出现的次数较多时,因为需要遍历找出对应该品类的词,所以花费的时间会增加,但整体上还是符合预期的。
如发现文章有错误、对内容有疑问,都可以关注美团技术团队微信公众号(meituantech),在后台给我们留言。
分享一线技术实践,沉淀成长学习经验