前言
在美团商家数据中心(MDC),有超过100w的已校准审核的POI数据(我们一般将商家标示为POI,POI基础信息包括:门店名称、品类、电话、地址、坐标等)。如何使用这些已校准的POI数据,挖掘出有价值的信息,本文进行了一些尝试:利用机器学习方法,自动标注缺失品类的POI数据。例如,门店名称为“好再来牛肉拉面馆”的POI将自动标注“小吃”品类。
机器学习解决问题的一般过程:
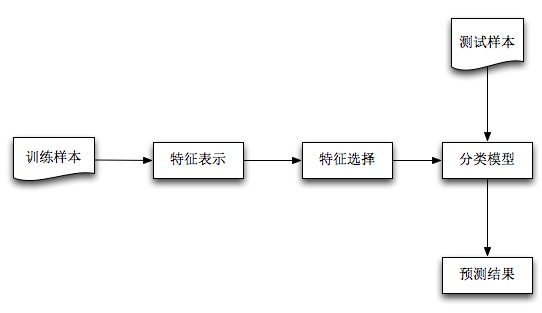
本文将按照:1)特征表示;2)特征选择;3)基于Naive Bayes分类模型;4)分类预测,四个部分顺序展开。
特征表示
我们需要先将实际问题转换成计算机可识别的形式。对于POI而言,反应出POI品类的一个重要特征是POI门店名称,那么问题转换成了根据POI门店名称判别POI品类。POI名称字段属于文本特征,传统的文本表示方法是基于向量空间模型(VSM模型)[1]:
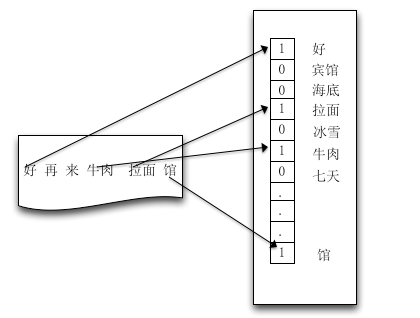
空间向量模型需要一个“字典”,这个字典可以在样本中产生,也可以从外部导入。上图中的字典就是[好, 宾馆, 海底, 拉面, 冰雪, ……. ,馆]。我们对已校准的POI,先利用Lucene的中文分词工具SmartCn[2]对POI名称做预分词处理,提取特征词,作为原始粗糙字典集合。
有了字典后便可以量化地表示出某个文本。先定义一个与字典长度相同的向量,向量中的每个位置对应字典中的相应位置的单词。然后遍历这个文本,对应文本中的出现某个单词,在向量中的对应位置,填入“某个值”(即特征词的权重,包括BOOL权重,词频权重,TFIDF权重)。考虑到一般的POI名称都属于短文本,本文采用BOOL权重。
在产生粗糙字典集合时,我们还统计了校准POI中,每个品类(type_id),以及特征词(term)在品类(type_id)出现的次数(文档频率)。分别写入到表category_frequency和term_category_frequency,表的部分结果如下:
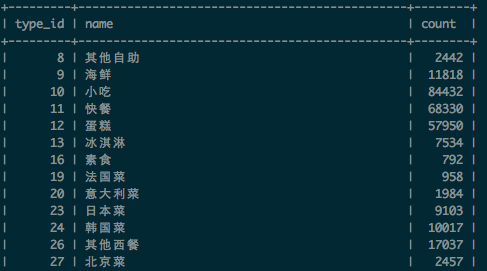
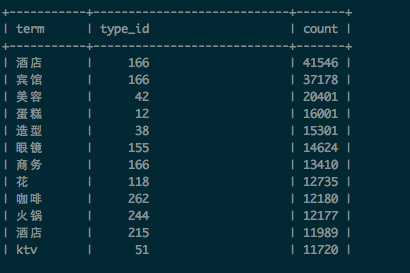
分别记:
A(i,j) = 特征词term(i) 在品类为type_id(j)出现的次数count
T(j) = 品类为type_id(j)在样本集出现的次数
N = 已校准POI数据集的数量
这些统计量,将在后续的计算中发挥它们的作用。
特征选择
现在,我们得到了一个“预输入字典”:包括了所有已校准POI名称字段的特征词,这些特征词比如:“88”、“11”, “3”、“auyi”、“中心”、“中国”、“酒店”、“自助餐”、“拉面”等。直观感觉,“88”、“11”, “3”、“auyi”、“中国”这些词对判断品类并没有多大帮助,但“酒店”、“自助餐”、“拉面”对判断一个POI的品类却可能起到非常重要作用。
那么问题来了,如何挑选出有利于模型预测的特征呢?这就涉及到了特征选择。特征选择方法可以分成基于领域知识的规则方法和基于统计学习方法。本文使用统计机器学习方法,辅助规则方法的特征选择算法,挑选有利于判断POI品类的特征词。
基于统计学习的特征选择算法
基于统计学习的特征选择算法,大体可以分成两种:
1.基于相关性度量(信息论相关) 2.特征空间表示(典型的如PCA)
文本特征经常采用的基于信息增益方法(IG)特征选择方法[3]。某个特征的信息增益是指,已知该特征条件下,整个系统的信息量的前后变化。如果前后信息量变化越大,那么可以认为该特征起到的作用也就越大。 那么,如何定义信息量呢?一般采用熵的概念来衡量一个系统的信息量:
$$[H(Y)=-\sum_{i=1}^{n}p\left ( y_{i}\right )\log p\left ( y_{i} \right )]$$
当我们已知该特征时,从数学的角度来说就是已知了该特征的分布,系统的信息量可以由条件熵来描述:
$$[H\left ( Y|X \right )=\sum _{x}p\left ( x \right )H\left ( Y|X=x \right )=-\sum _{x}\sum _{y}p\left ( x,y \right )\log p\left ( y|x \right )]$$
该特征的信息增益定义为:
$$[IG(X)=H(Y)-H(Y|X)]$$
信息增益得分衡量了该特征的重要性。假设我们有四个样本,样本的特征词包括“火锅”、“米粉”、“馆”,我们采用信息增益判断不同特征对于决策影响:
| 米粉(A) | 火锅(B) | 馆© | 品类 |
|---|---|---|---|
| 1 | 1 | 0 | 火锅 |
| 0 | 1 | 1 | 火锅 |
| 1 | 0 | 0 | 小吃 |
| 1 | 0 | 1 | 小吃 |
整个系统的最原始信息熵为:
$$[H\left ( Y \right )=-\sum _{i=1}^{2}p\left ( y_{i} \right )\log p\left ( y_{i} \right )=-2*\frac{1}{2}*\log \frac{1}{2} = 1]$$
分别计算每个特征的条件熵:
$$[H\left ( C|A \right )=-\sum_{i=1}^{2}\sum_{j=1}^{2}p\left ( x,y \right )\log p\left ( y|x \right )=0-0- \frac{1}{2}\log \frac{2}{3} -\frac{1}{4}\log \frac{1}{3} =0.69]$$
利用整个系统的信息熵减去条件熵,得到每个特征的信息增益得分排名(“火锅”(1) > “米粉”(0.31) > “馆”(0)) ,按照得分由高到低挑选需要的特征词。
本文采用IG特征选择方法,选择得分排名靠前的N个特征词(Top 30%)。我们抽取排名前20的特征词:[酒店, 宾馆, 火锅, 摄影, 眼镜, 美容, 咖啡, ktv, 造型, 汽车, 餐厅, 蛋糕, 儿童, 美发, 商务, 旅行社, 婚纱, 会所, 影城, 烤肉]。这些特征词明显与品类属性相关联具有较强相关性,我们将其称之为品类词。
基于领域知识的特征选择方法
基于规则的特征选择算法,利用领域知识选择特征。目前很少单独使用基于规则的特征选择算法,往往结合统计学习的特征选择算法,辅助挑选特征。
本文需要解决的是POI名称字段短文本的自动分类问题,POI名称字段一般符合这样的规则,POI名称 = 名称核心词 + 品类词。名称核心词对于实际的品类预测作用不大,有时反而出现”过度学习“起到负面作用。例如”好利来牛肉拉面馆“, ”好利来“是它的名称核心词,在用学习算法时学到的很有可能是一个”蛋糕“品类(”好利来“和”蛋糕“品类的关联性非常强,得到错误的预测结论)。
本文使用该规则在挑选特征时做了一个trick:利用特征选择得到的特征词(绝大部分是品类词),对POI名称字段分词,丢弃前面部分(主要是名称核心词),保留剩余部分。这种trick从目前的评测结果看有5%左右准确率提升,缺点是会降低了算法覆盖度。
分类模型
建模
完成了特征表示、特征选择后,下一步就是训练分类模型了。机器学习分类模型可以分成两种:1)生成式模型;2)判别式模型。可以简单认为,两者区别生成式模型直接对样本的联合概率分布进行建模:
生成式模型的难点在于如何去估计类概率密度分布p(x|y)。本文采用的朴素贝叶斯模型,其”Naive”在对类概率密度函数简化上,它假设了条件独立:
$$[p\left ( y|x \right )=\frac{p\left ( y \right )p\left ( x|y \right )}{p\left ( x \right )} \sim p\left ( x|y \right )]$$
根据对p(x|y)不同建模形式,Naive Bayes模型主要分成:Muti-variate Bernoulli Model (多项伯努利模型)和Multinomial event model(多项事件模型)[4]。一次伯努利事件相当于一次投硬币事件(0,1两种可能),一次多项事件则相当于投色子(1到6多种可能)。我们结合传统的文本分类解释这两类模型:
多项伯努利模型
已知类别的条件下,多项伯努利对应样本生X成过程:遍历字典中的每个单词(t1,t2…t|V|),判断这个词是否在样本中出现。每次遍历都是一次伯努利实验,|V|次遍历:
$$p(X|C_{j})=\prod_{i=1}^{|V|}=1(t_{i}\in X)p(t_{i}|C_{j}) %2B 1(t_{i}\notin X)(1-p(t_{i}|C_{j}))$$
其中1(condition)为条件函数,该函数表示当条件成立是等于1,不成立时等于0;|V|则表示字典的长度。
多项事件模型
已知类别的条件下,多项事件模型假设样本的产生过程:对文本中第k个位置的单词,从字典中选择一个单词,每个位置k产生单词对应于一次多项事件。样本X=(w1,w2…ws)的类概率密度:
$$[p(X|C_{j})=p(w_{1},w_{2},w_{3}…w_{s}|C_{j})=\prod_{i=1}^{s}p(w_{i}|C_{j})]$$
采用向量空间模型表示样本时,上式转成:
$$[p(X|C_{j})=\prod_{i=1}^{|V|}p(t_{i}|C_{j})^{N(t_{i},X)}]$$
其中N(ti,X) 表示特征词i在样本X出现的次数。
参数估计
好啦,一大堆无聊公式的折磨后,我们终于要见到胜利的曙光:模型参数预估。
一般的方法有最大似然估计、最大后验概率估计等。本文使用的是多项伯努利模型,我们直接给出多项伯努利模型参数估计结论:
$$[\Theta _{j}=p(y=C_{j})=\frac{\sum_{k=1}^{N}1(y_{k}=C_{j})}{\sum_{k=1}^{N}\sum_{j=1}^{C}1(y_{k}=C_{j})}=\frac{T\left ( j \right )}{N}]$$
$$[\Theta _{i|j}=p\left ( t_{i}|C_{j} \right )=\frac{\sum_{k=1}^{N}1(y_{k}=C_{j}1(t_{i}\in C_{j}))}{\sum_{k=1}^{N}1(y_{k}=C_{j})}=\frac{A(i,j)}{N}]$$
还记得特征表示一节中统计的term_category_frequency和category_frequency两张表吗?此时,就要发挥它的作用了!我们,只需要查询这两张表,就可以完成参数的估计了,是不是很happy?
过程虽然有点曲折,但是结果是美好的~ 具体参数意义可以参见特征表示一节。
接下来的coding的可能需要关注的两个点:
参数平滑
在计算类概率密度p(X | Cj)时,如果在类Cj下没有出现特征ti ,p(ti | Cj)=0,类概率密度连乘也将会等于0,额,对于一个样本如果在某条件下某个特征没有出现,便认为她产生的可能等于零,这样的结论实在是过武断,解决方法是加1平滑:
其中,|C|表示样本的类别数据。
小数溢出
在计算类概率密度时多个条件概率(小数)连乘,会存在着超过计算机能够表示的最小数可能,为避免小数溢出问题,一般将类概率密度计算转成成对数累和的形式。
$$[\log p(X|C_{j})=\log p(t_{1},t_{2},t_{3}…t_{|V|}|C_{j})=\sum_{i=1}^{|V|}\log p\left ( t_{i}|C_{j} \right )]$$
另外,如果在计算p(ti | Cj)时过小,取对数后将会得到一个负无穷的值,需要对p(ti | Cj)截断处理:小于某个阈值(如1E-6)时,采用该阈值替代。
算法预测
本节将结合前面三节内容,给出算法具体的计算预测过程。为简化问题,我们假设字典为:[拉面,七天,牛肉,馆],并且只有火锅和快餐两个品类,两类样本的数量均为8个。以“好 利 来 牛肉 拉面 馆为例”:
- 对测试样本做中文分词,判断”牛肉“属于品类词,丢弃品类词”牛肉“前面的部分,并提取样本的特征词集合得到:[牛肉 拉面 馆]
- 根据字典,建立向量空间模型:x = [1, 0, 1, 1]
- 利用Naive Bayes模型分类预测,我们给出火锅和快餐两类样本的term_category_frequency统计:
| 特征词\品类 | 火锅(C1) | 快餐(C2) |
|---|---|---|
| 拉面 | 0 | 5 |
| 七天 | 2 | 0 |
| 牛肉 | 4 | 2 |
| 馆 | 2 | 1 |
样本属于快餐的概率高于属于火锅概率4倍,预测样本属于快餐置信度明显高于火锅概率。
算法随机抽取2000条未校准的POI数据进行评测,算法的评测指标有两个:覆盖度和准确率。覆盖度是指算法可预测的样本数量在整个测试样本集中的比例。由于采用特征选择后,一些POI名称因不包含特征词集合而无法预测,算法的评测的覆盖度为84%。算法的准确率是指,可预测正确样本在整个测试样本集中的比例,算法评测的正确率为91%。
总结
- 机器学习解决问题最关键的一步是找准问题:这种问题能否用机器学习算法解决?是否存在其他更简单的方法?简单的如字符串匹配,利用正则就可以简单解决,才机器学习方法反而很麻烦,得不偿失。
- 如果能机器学习算法,如何去表示这个机器学习问题,如何抽取特征?又可能归类哪类机器模式(分类、聚类、回归?)
- 找准问题后,可以先尝试一些开源的机器学习工具,验证算法的有效性。如果有必要,自己实现一些机器算法,也可以借鉴一些开源机器学习算法实现。
如发现文章有错误、对内容有疑问,都可以关注美团技术团队微信公众号(meituantech),在后台给我们留言。
分享一线技术实践,沉淀成长学习经验